Adott az alábbi ábrán szereplő darts-tábla.
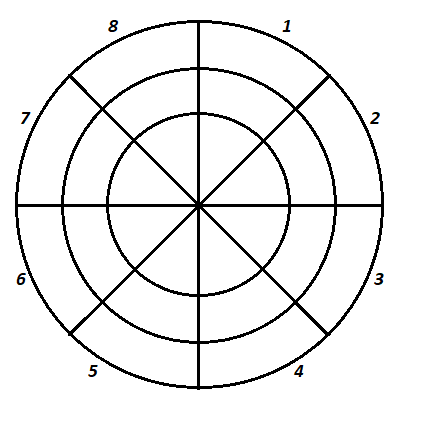
A táblán 1-8 számokkal jelöltük az egyes körcikkeket. Minden körcikk három részből áll.
Az egyes körgyűrűket nem jelöltük külön betűkkel: ezekre a továbbiakban külső, középső, belső körként fogunk hivatkozni.
A feladatunk, hogy a tábla minden egyes mezőjét (a körgyűrűcikkeket) töltsük ki zöld vagy piros színnel úgy, hogy az alábbi szabályoknak megfeleljenek:
1. Minden mező vagy zöld, vagy piros.
2. A táblán összesen 14 zöld mező található.
3. A külső körgyűrűben kevesebb zöld mező található, mint a középsőben.
4. Az 1-es az egyetlen körcikk, amelynek mindhárom köre (külső, középső, belső) zöld színű.
5. Sem a külső, sem a középső, sem a belső körben nincs egymást követő három olyan szomszédos mező, amely színe azonos lenne.
6. Minden egyes körre (külső, középső, belső) igaz, hogy a 8 osztóit tartalmazó sorszámú mezők közül pontosan kettő zöld, és pontosan kettő piros.
Sőt, még azt is elárulom, hogy ha megmondanám, hogy hány olyan körcikk van, amelynek a külső és a belső körében is piros mező található, meg tudnád adni az egyetlen lehetséges megoldást.
Mi ezt az egyetlen lehetséges megoldást kérjük a 10 pontért.
Szokásunktól eltérően levezetést nem kérünk, ám elakadás esetén segíteni elsősorban annak tudunk, aki a gondolatmenetének főbb pontjait felvázolja.