Binomiélis tétel

Legyen n természetes szám, a és b pedig valós számok. Ekkor igaz a következő, ún. binomiális tétel:

$(a+b)^n = \sum_{k=0}^n {n \choose k} a^{n-k}b^{k}$ .

Tehát a fenti formula megmutatja, hogyan kell két tag összegét (ún. binomot) n-edik hatványra emelni. Ez a kombinatorika talán legklasszikusabb eredménye.
A formula eredete a XI. századig nyúlik vissza. Omar Khajjam perzsa matematikus már ismerte a tételt. Newton vette észre, hogy a binomiális formula kiterjeszthető negatív, illetve nemcsak egész kitevők esetére is. Sokan az ő nevéhez kapcsolják a binomiális tételt.

Példák:

Ha a=b=1, akkor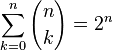

$\sum_{k=0}^{n} { n \choose k } = 2^n$ .

Ha a=1 és b=-1, akkor

$\sum_{k=0}^{n} (-1)^k { n \choose k } = 0$ .

Szerzők: jarod12

Figyelmeztetés!! Ezt a szócikket még nem ellenőriztük!

[Szócikk szerkesztése]
[Lexikon kezdőlapra lépés]

Friss feladványok:
Periódusos szavak - kicsit másképp 2.
Csak a kezeMet figyeld!
Szakmai anagramma 52.
Szétválogatás 2. (korrigálva)
Mi a nevem? (2.)
Tekercs
Meg egy Y

Hirdetés

impresszum :: médiaajánlat :: segítség :: ajánló :: kezdőlapnak :: kedvencekhez