|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Friss fórum:
|
|
|
|
A hét kérdése:
Jelentkezz be a heti kérdéshez!
|
|
|
|
Legolvasottabbak:
|
|
Varázs-szög
2025-12-13 6:55
A háromszög oldalösszegei
Nehéz, beküldte:
beke*, szerkesztő: Sandviking
Háromszög alakban 12 kör látható az ábrán, az 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 számokkal feltöltve. A számok összege mindhárom oldal mentén 32.
A sarokszámok: 3,7 és 8. A három sarokszám azonosítja be a kitöltést, piros színnel ez is látható az ábrán.
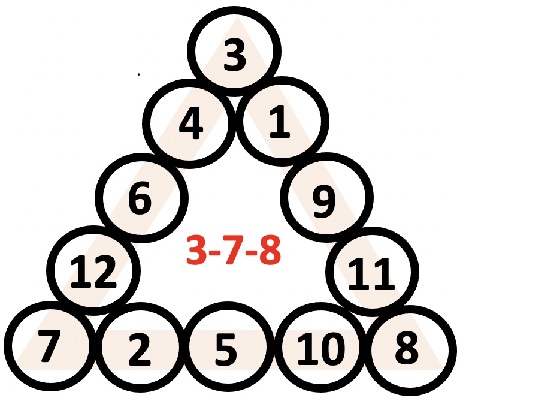
Ilyen módon kitöltött háromszögekkel kapcsolatos ez a feladat.
Azt tudhatjuk, hogy bizonyos feltételt teljesítő sarokszámok esetén az ilyen típusú ábra biztosan kitölthető, több tucatnyi megoldása van (76 db). Az ábra is bizonyítja, hogy a 3-7-8 azonosítójú háromszög kitölthető.
Az is megállapítható, hogy az oldalak mentén szereplő közbenső számok sorrendje lényegtelen, csak az összegük a lényeges. A sarokszámok sorrendje is lényegtelen. Különbözőnek (egyedinek) azokat a kitöltéseket nevezzük, ahol az sarokszámok különböznek. Ezeket az egyedi megoldásokat vizsgálva válaszolj a következő kérdésekre, minden esetben némi indoklással.
(1) milyen feltételnek kell megfelelni a sarokszámoknak? (1 pont),
(2) mely sarokszámokra lesz az oldalösszeg a legkisebb? (1 pont),
(3) mely sarokszámokra lesz az oldalösszeg a legnagyobb? (1 pont),
(4) hány egyedi megoldás van, ahol mindhárom sarokszám prím? (2 pont),
(5) hány egyedi megoldás van, ahol az oldalösszeg prím? (4 pont).
(6) A kérdésekhez kapcsolódó (de legfeljebb 4 darab) háromszög esetében add meg a háromszög számait is óramutató járás szerinti sorrendben, a felső (ez legyen egyúttal a legkisebb) sarokszámmal kezdődően. (1-1 pont, maximum 4 pont).
Tehát a pipához legalább egy teljes táblát is ki kell tölteni
10 ponttól pipa.
A beküldési határidő lejárt, a regisztrálatlanul beküldött új megoldásokat már nem értékeljük! Új hozzászólás beküldése (már csak regisztráltan beküldött megoldást értékeljük)
| A Varázs-szög című feladvány statisztikája: |
| A feladványt eddig 903 felhasználó olvasta, és 39 megoldást küldtek be rá. |
| A feladványt 15 látogató fejtette meg helyesen. | Akik helyes megfejtést küldtek be (vastaggal aki határidőn belül):
Anikóka, AtomHangya, bolnyi, cdiv, hata, horsa, Kuala13, mbela, mihtoth, mutterka, ocotillo, saja, szedit24, szmoni65, Tucatka |
| | Ajánld a feladványt másoknak: |
|
|
Ha be lennél jelentkezve, itt megnézhetnéd a beküldött megoldásokat
|
|
|